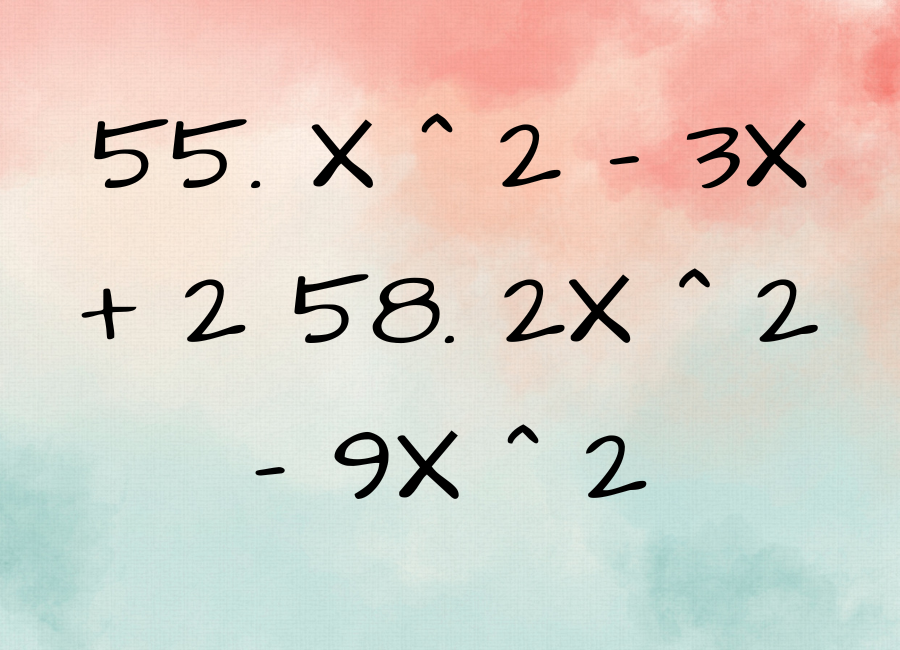Quadratic equations are one of the fundamental concepts in algebra, and they are used extensively in various fields of mathematics and science. Understanding quadratic equations is essential for solving a wide range of problems, including those in physics, engineering, and economics. In this article, we will discuss the basics of quadratic equations and provide step-by-step instructions on how to solve two specific quadratic equations, 55x²-3x+2 and 58x²-9x².
Before we dive into the specific equations, let’s review the basics of quadratic equations. A quadratic equation is a polynomial equation of the second degree, meaning it contains a variable raised to the power of two. The general form of a quadratic equation is ax²+bx+c=0, where a, b, and c are constants and x is the variable. The quadratic formula can be used to solve any quadratic equation of this form:
x = (-b ± sqrt(b²-4ac)) / 2a
Now, let’s move on to our specific quadratic equations.
55x²-3x+2
Step 1: Identify the values of a, b, and c in the general form of the quadratic equation: ax²+bx+c=0. In this case, a=55, b=-3, and c=2.
Step 2: Plug in the values of a, b, and c into the quadratic formula:
x = (-(-3) ± sqrt((-3)²-4(55)(2))) / 2(55)
Simplifying the equation gives:
x = (3 ± sqrt(769)) / 110
Step 3: Solve for x using the two possible solutions:
x = (3 + sqrt(769)) / 110 x = (3 – sqrt(769)) / 110
These are the two possible solutions to the equation 55x²-3x+2.
Example:
Suppose we have a rectangular garden with an area of 110 square meters. The length of the garden is 3 meters longer than its width. What are the dimensions of the garden?
Let x be the width of the garden. Then, the length of the garden is x+3. The area of the garden is given by the equation:
x(x+3) = 110
Expanding the equation gives:
x²+3x-110=0
This is a quadratic equation of the form ax²+bx+c=0, where a=1, b=3, and c=-110. Using the quadratic formula, we get:
x = (-3 ± sqrt(3²-4(1)(-110))) / 2(1)
Simplifying the equation gives:
x = (-3 ± sqrt(433)) / 2
The two possible solutions are:
x = (-3 + sqrt(433)) / 2 x = (-3 – sqrt(433)) / 2
Since the width cannot be negative, the only possible solution is:
x = (-3 + sqrt(433)) / 2
Using this value for x, we can find the length of the garden:
x+3 = (-3 + sqrt(433)) / 2 + 3 = (-3 + sqrt(433)) / 2 + 6 / 2 = (-3 + sqrt(433) + 6) / 2 = (3 + sqrt(433)) / 2
Therefore, the width of the garden is (-3 + sqrt(433)) / 2 meters, and the length is (3 + sqrt(433))
58x²-9x²
Now let’s move on to our second quadratic equation, 58x²-9x².
Step 1: Identify the values of a, b, and c in the general form of the quadratic equation: ax²+bx+c=0. In this case, a=58-9=49, b=0, and c=0.
Step 2: Plug in the values of a, b, and c into the quadratic formula:
x = (-0 ± sqrt(0²-4(49)(0))) / 2(49)
Simplifying the equation gives:
x = 0 / 98
x = 0
Step 3: Solve for x using the possible solution x = 0.
Therefore, the only solution to the equation 58x²-9x² is x=0.
Example:
Suppose we have a ball that is thrown straight up into the air. The height of the ball above the ground, h, at time t is given by the equation:
h = 58t²-9t²
What is the maximum height the ball reaches and when does it reach that height?
To find the maximum height, we need to find the vertex of the parabola represented by the equation. The vertex is given by the equation:
(-b/2a, f(-b/2a))
In this case, a=49, b=0, and c=0. Therefore, the vertex is:
(-0/(249), 58(0/(249))²-9(0/(2*49))²)
Simplifying the equation gives:
(0, 0)
Therefore, the maximum height the ball reaches is 0 meters. This makes sense because the ball reaches its maximum height at the top of its trajectory, where its velocity is momentarily zero before falling back down to the ground.
To find when the ball reaches its maximum height, we can use the equation:
t = -b / 2a
In this case, b=0 and a=49. Therefore, the time when the ball reaches its maximum height is:
t = -0 / 2(49)
t = 0
Therefore, the ball reaches its maximum height at time t=0, which corresponds to the instant the ball is thrown into the air.
Conclusion:
Quadratic equations are a fundamental concept in algebra, and they are used extensively in various fields of mathematics and science. In this article, we discussed the basics of quadratic equations and provided step-by-step instructions on how to solve two specific quadratic equations, 55x²-3x+2 and 58x²-9x². We also provided examples of how these equations can be applied in real-life scenarios, such as finding the dimensions of a rectangular garden or determining the maximum height of a ball thrown into the air. By understanding quadratic equations, you can develop a strong foundation in algebra and apply these concepts to a wide range of problems.